Introdução
Muitas vezes não nos importamos com a questão: pagar à vista ou à prazo, simplesmente escolhemos a que “cabe no meu bolso”, seja por realmente não nos importarmos ou não levar em conta uma questão interessante: Quanto a mais estou pagando por ter feito esta escolha?
A grande questão está na relação entre juros e o tempo. Quando a opção é parcelar uma compra, você estará pagando pelo “empréstimo” que inconscientemente acaba fazendo. Ao adquirir na data de hoje 100% do produto e pagar só uma parcela, correspondente por exemplo a 20% do mesmo, certamente haverá juros embutidos no preço, pois o detentor do produto está de uma forma indireta te fazendo um empréstimo.
Parece simples, mas pode ter suas complicações. Vamos aprender um pouco mais sobre juros!?

Juros Simples
Baseando-se nos conceitos de juros simples para calcular um valor final em uma situação, se está apenas considerando que o capital inicial rende juros. Por este método, não é calculado o famoso “juros sobre juros”. A equação que dará este valor de juros é a seguinte:
J = P . i . n
onde:
- P – principal;
- J – juros;
- i – taxa de juros;
- n – número de períodos.
O valor final que será obtido, depois do chamado período de capitalização é o valor futuro e é dado por:
F = P + J, mas como J=P.i.n então: F = P + P.i.n o que resulta: F = P(1 +i.n)
Sendo :
- F – Valor futuro.
Este método de cálculo é pouquíssimo utilizado no mercado, já que o padrão que se adota é o calculo de juros compostos.

Juros Compostos
Sob a ótica dos juros compostos, ao fim de cada período ocorre a adição do juro ao principal, sendo que dessa forma, esse valor também irá render juros no próximo período. Matematicamente isso resultará em:
Para o primeiro período teremos:
F1 = P + P . i = P . (1 + i)
Para o segundo período teremos:
F2 = F1 + F1 . i = F1 . ( 1 + i) = P . (1 + i).(1 + i) = P . (1 + i)²
Para o terceiro período teremos:
F3 = F2 + F2.i = F2 . (1 + i) = P . (1 + i)². (1 + i) = P . (1 + i)³
E assim por diante. Do apresentado pelas equações acima, pode-se supor que para um período “n” o cálculo dos juros compostos será dado por:
F = P . (1 + i)n
Fluxo de caixa
Nada mais é do que a representação gráfica das receitas e despesas, durante um determinado intervalo de tempo. A figura abaixo ilustra um fluxo de caixa. No período 0 da vida do projeto, tem-se a despesa de investimento. Nos períodos subseqüentes, tem-se tanto receitas quantos despesas, relativas a recebimentos por determinado produto ou serviço e as despesas inerentes do processo. No período n, que seria o fim da vida do projeto, há o valor residual.
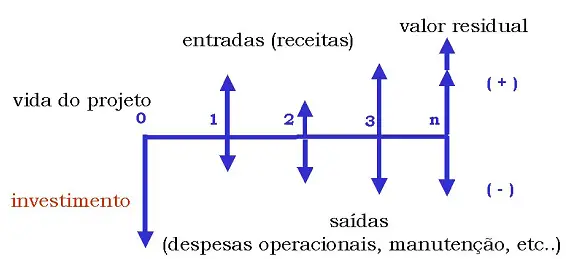
Um ponto importante é que os gráficos de fluxo de caixa mostram a ótica de quem faz a análise. O fluxo de caixa segundo a ótica do comprador é diferente do fluxo na ótica do vendedor.
Grande parte do trabalho envolvendo os fluxos de caixa está na obtenção das chamadas relações de equivalência. Para saber mais sobre elas, continue lendo o nosso próximo artigo relacionado nos links abaixo.
Artigos Relacionados
Noções em Engenharia econômica
Tabelas das relações de equivalência
>> Conceitos importantes de economia: Juros e Fluxo de caixa
Taxas e relações de equivalência








Pingback: Relações de equivalência (séries gradiente e perpétua) | Economia - Bico do Corvo
Pingback: Tabelas das relações de equivalência - economia e dinheiro | Economia - Bico do Corvo
Pingback: Taxas e relações de equivalência - economia e dinheiro | Economia - Bico do Corvo
Pingback: Relações de equivalência (P/F, P/A e F/A) | Economia - Bico do Corvo